Glass Transition Data (only for DSC Curing)

For projects of type DSC Curing, it is possible to define the glass transition temperatures T_g as a function of the conversion α (degree of curing). The mathematical interpolation of these data can be utilized to simulate glass transition temperatures as a function of time or temperature.

Click on Glass Transition Data:

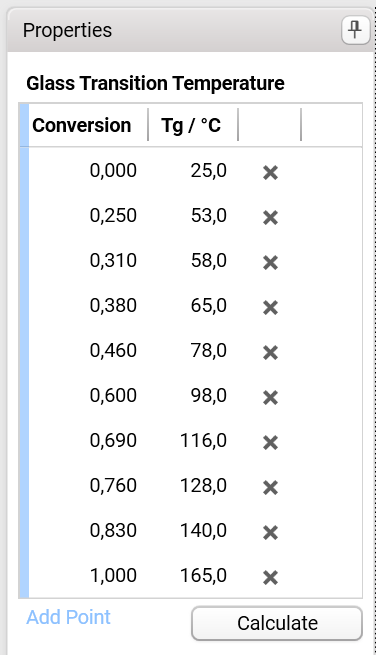
In Properties, one can add T_g data points (conversion α and T_g for this conversion), edit them or delete T_g data points. At least one T_g data point is required. See remark below regarding how to determine T_g(α) from DSC measurements.

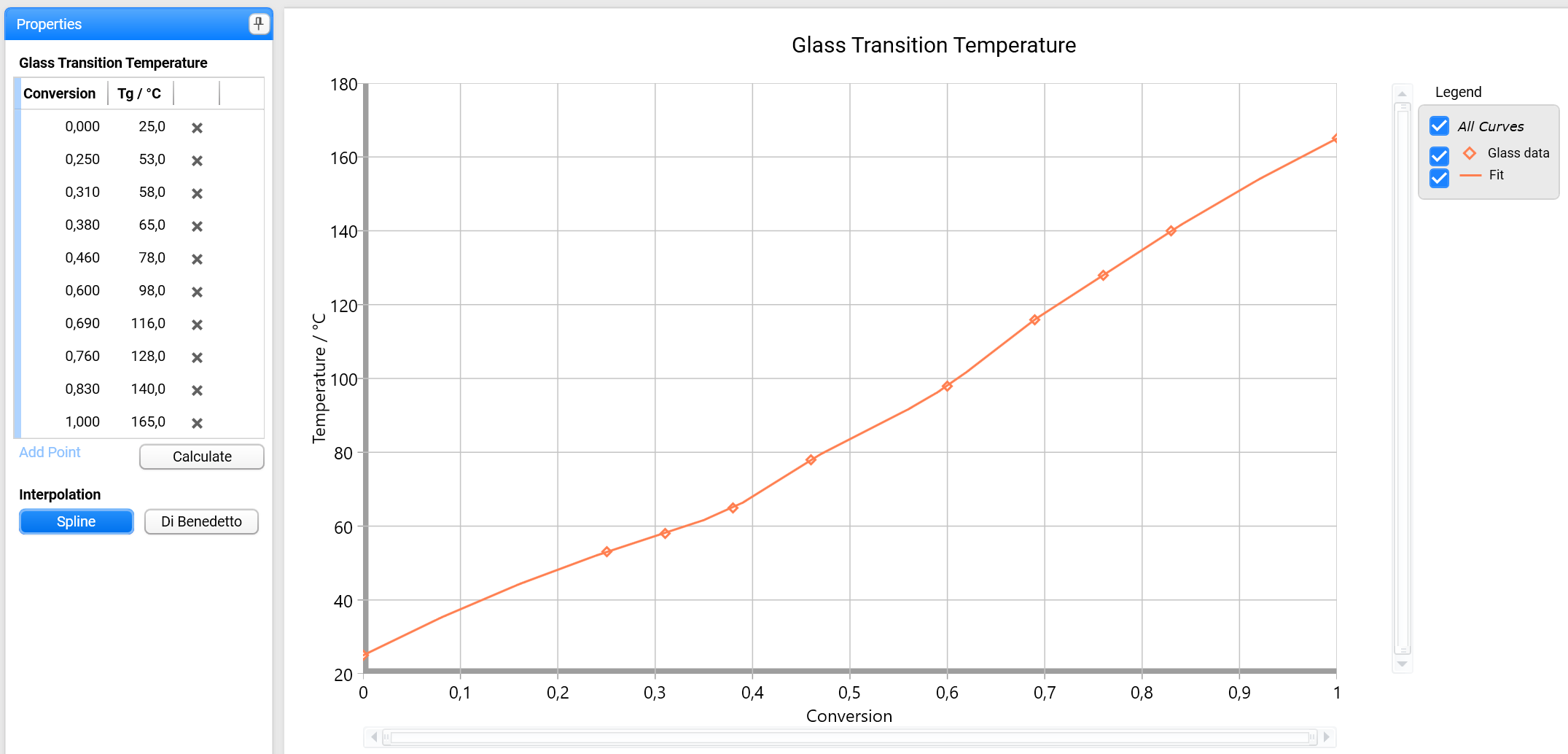
Press Calculate for a new calculation of the interpolation or an update.

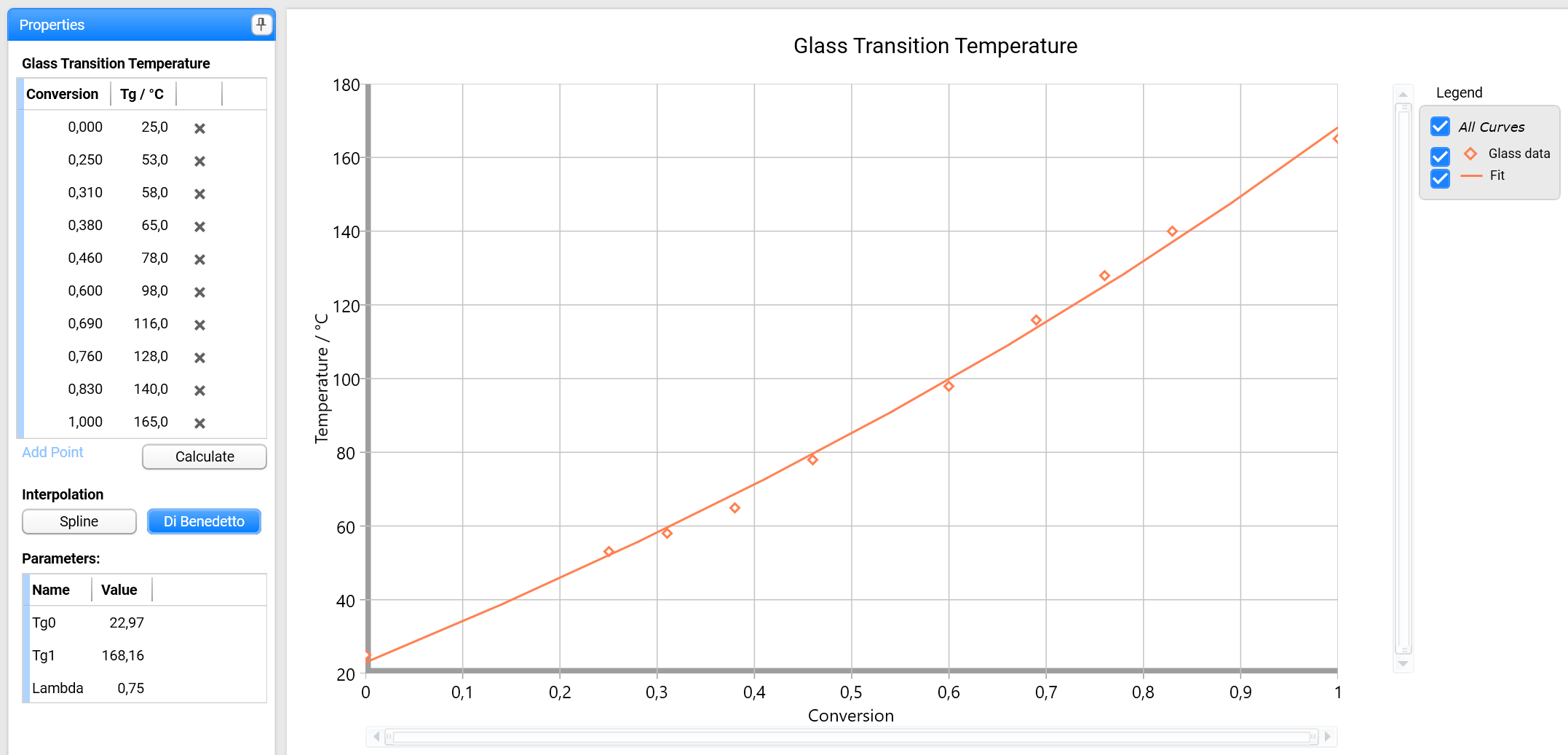
For one T_gdata point, the interpolation is a constant over the entire conversion range. Two T_gdata points always lead to a line and three T_g data points to a parabola. If more than three T_g data points are given and interpolation type Spline is selected, a spline is calculated.

Example

Di Benedetto as interpolation type uses Di Benedetto’s equation for the fit of T_gas a function of the conversion α:

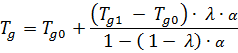
The parameters T_g0 and T_g1are the glass transition temperatures at α=0 and α=1. The parameter λ determines the curvature of the fit, which can have only one direction in case of Di Benedetto as interpolation type.

Example

Note: How to determine the glass transition temperature T_g as a function of the conversion α from DSC measurements:

Heating of the first, completely uncured sample to a sufficiently high temperature so that T_g(α=0)and also the entire curing effect are detected; the enthalpy of this exothermic curing effect is ∆H_tot. Then, this fully cured sample is cooled down again and heated a second time revealing T_g(α=1).

Further T_g(α) data is determined in the following way: For each T_g(α) data point, a new completely uncured sample is heated only to temperatures where curing has started but is not yet complete. Then this sample is cooled down again, and heated up a second time to the temperature where curing is fully completed; the enthalpy of this exothermic curing effect in the second heating is ∆H. The glass transition temperature observed in the second heating is T_g(α) and the corresponding α is equal to (∆H_tot-∆H) / ∆H_tot. Adjustment of the maximum temperature of the first heating obviously allows for variation of α; the higher the maximum temperature, the higher is the value of α.